
by Gerald Newton
November 3, 1999
The diagrams below show just how simple three phase power can be. American electricians are fortunate that power frequencies are established at 60 hertz and take the form of the common sine wave. Engineers, on the other hand, are quite unfortunate since they must learn electrical theory for any frequency and wave form, and for power factors other than unity. But this article is not for engineers, it is for the American electrician so calculus is not going to be included in this discussion. However, electricians are expected to know geometry, trigonometry, algebra and arithmetic. The diagrams below are an attempt to provide a simple understanding of three phase power systems such as seen with 208/120 volt and 480/277 volt three phase, 4 wire systems. We already know by common electrical knowledge that the neutral current in a balanced three phase system is 0 amperes for resistive loads such as incandescent lighting and heaters where the power factor is approximately 1.0. We also know that in a balanced three phase system the neutral current is approximately equal to the line current for electric discharge lighting loads such as high pressure sodium lights or fluorescent lights because of third harmonics.
For systems where the line currents are not equal there is a simple method for finding the neutral current. We can convert A phase, B phase and C phase into polar coordinates where the amperes are represented by vectors then add the three vectors to find the approximate neutral current and phase angle. This is called geometric vector addition.
Mathematically, we can precisely add the three vectors for the line currents by converting vectors into their horizontal and vertical components by using trigonometry. We can add the horizontal components, then add the vertical components, then convert this to polar coordinates to find the sum of the vectors. This is called algebraic vector addition.
We will do the geometric addition using the root mean square values of the sine wave. The second part of this discussion will cover algebraic addition.
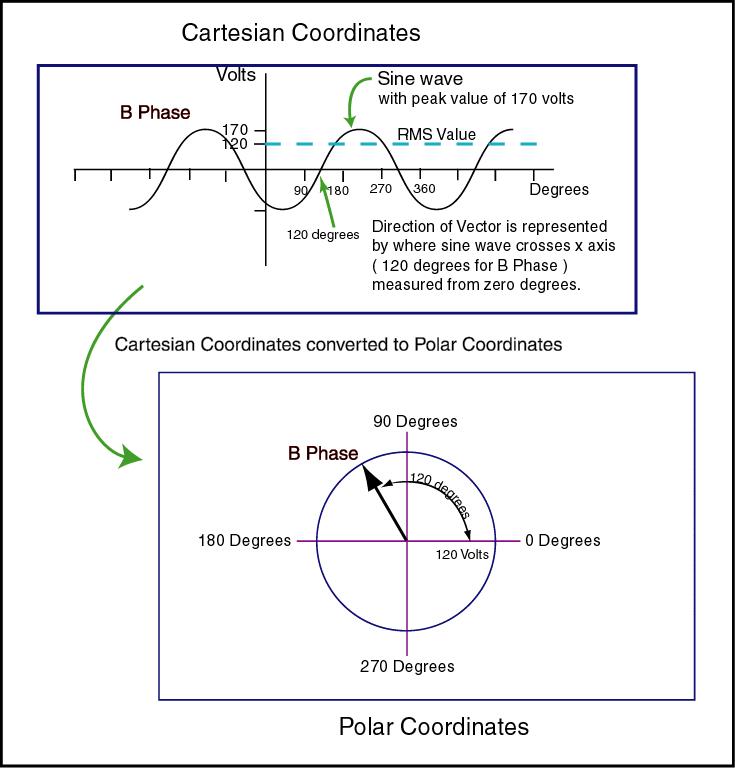
First let us convert cartesian coordinates or the familiar
X Y type graph to a Polar graph as demonstrated below.

So what about B Phase? Well here it is!
Combining A phase, B phase, and C Phase.....

That looks easy enough and is. We have all learned a little about
vectors, I am sure. A Vector is a line that represents magnitude
(its length) and has direction. The direction is referenced to zero
degrees and that is usually a horizontal line that parallels this sentence.
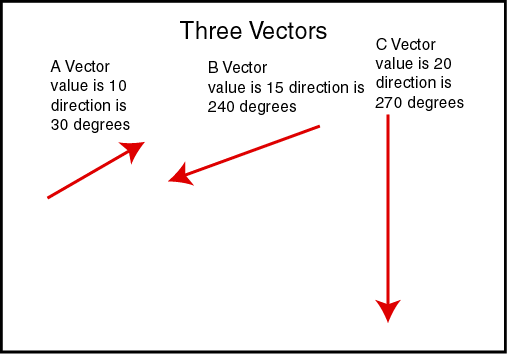
For example below is the phase vectors representing a line current of 30 amperes for each phase.

Our next step is to add the vectors. The neutral current is the sum of the A phase, B phase, and C phase vectors. So how do we add vectors? Actually, there is a very simple, easy, and fast method that gives a good approximation. Simply place each vector on the end of the preceding vector, then draw a line from the center point where the magnitude value is zero to the end of the final vector. It is done like this:

The approximate value of the Sum is 20 plus something and the direction is about 260 degrees. We could get much better results using polar graph paper and a ruler to scale the values.
We can do the same thing with the three phase vectors that represent
current as shown below.
In this example the vectors represent equal line currents of 30 amperes.
The neutral current should be zero and sure enough, the sum of the phase
currents add up to a vector of zero magnitude. The direction is irrelevant.
Remember, the neutral current is the sum of the three vectors that represent
the phase line currents.

Now let us try this approximation method to add three phase line currents that are not equal.

| Click the mouse button to place several vectors on the screen. Then click on action to sum them up. The vector is the sum is the white vector from the origin to the head of the last vector. | |
|
|
Use the mouse button to lay down up to ten vectors. Click on the Action button to sum the up. |