
by Gerald Newton
November 5, 1999
The geometric addition of vectors gives a fast approximation of neutral current in a three phase system. A more precise calculation can be performed using algebra. This can be a long mathematical problem, but by restricting our calculation to A phase at 0 degrees, B phase at 120 degrees, and C phase at 240 degrees the calculation is simplified.
The figure below demonstrates how to break a vector down into its horizontal (X) and vertical (Y) components. The magnitude of the vector is its length in whatever units we chose to represent. In our case that would be amperes.

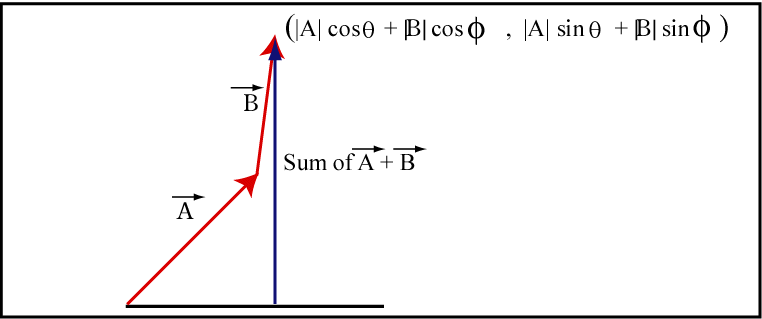
The following figures demonstrates the algebraic addition of two vectors.

The Pythagorean is used to find the algebraic value
of a vector once its X and Y components are known.

The following demonstrates the use of the Pythagorean
theorem to find the magnitude of the sum of two vectors.

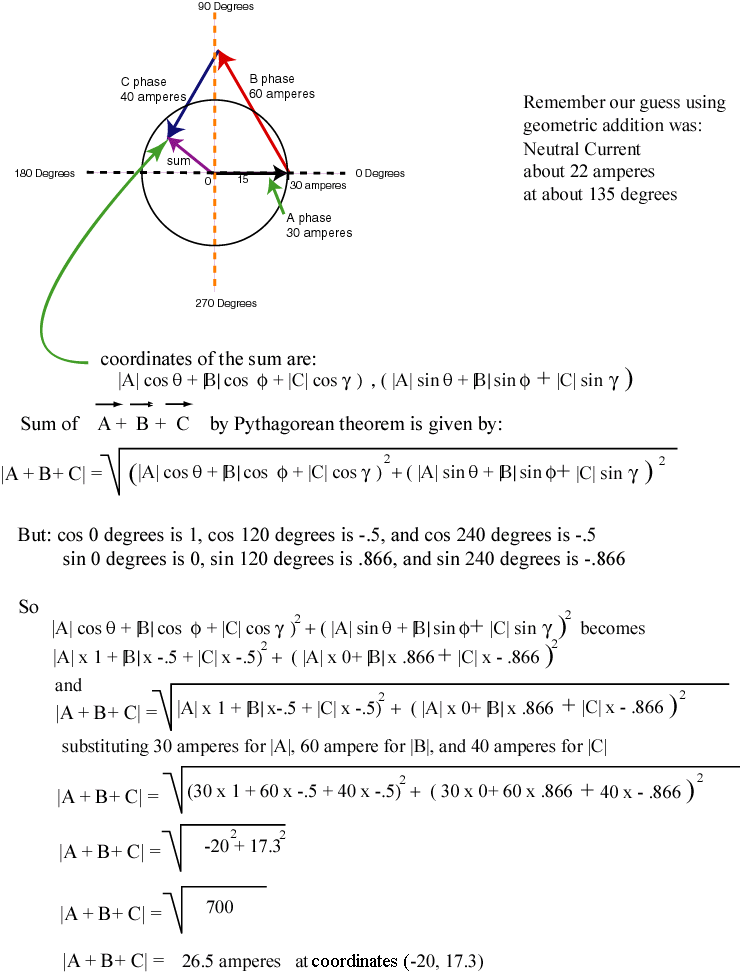
For three vectors the magnitude calculation is similar
to that for two vectors. A third component is added for the third
vector. The process of multiplying the polynomials can be reduced
by using the known angles for the A phase, B phase, and C phase vectors.
The sines and cosines are known for the three angles, 0 degrees, 120 degrees,
and 240 degrees.
Calculator by electrician2.com |
|||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
Use the mouse button to lay down up to ten vectors. Click on the Action button to calculate the sum. |